ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ΄ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ
ΠΑΡΑΣΚΕΥΗ 5 ΙΟΥΛΙΟΥ 2002 - ΑΕΠΠ

ΘΕΜΑ 1ο
Α. Να γράψετε στο τετράδιό σας τον αριθµό κάθε πρότασης και δίπλα τη λέξη Σωστό, αν είναι σωστή, ή τη λέξη Λάθος, αν είναι λανθασµένη.
Μονάδες 12
1. Η τιµή µιας µεταβλητής δεν µπορεί να αλλάξει κατά τη διάρκεια εκτέλεσης ενός αλγόριθµου.
2. Με τον όρο δεδοµένο αναφέρεται οποιοδήποτε γνωσιακό στοιχείο προέρχεται από επεξεργασία δεδοµένων.
3. Σκοπός της συγχώνευσης δύο ταξινοµηµένων πινάκων είναι η δηµιουργία ενός τρίτου ταξινοµηµένου πίνακα, που περιέχει τα στοιχεία των δύο πινάκων.
4. Τα λογικά λάθη είναι συνήθως λάθη σχεδιασµού και δεν προκαλούν τη διακοπή της εκτέλεσης του προγράµµατος.
5. Σε ένα µεγάλο και σύνθετο πρόγραµµα, η άσκοπη χρήση µεγάλων πινάκων µπορεί να οδηγήσει ακόµη και σε αδυναµία εκτέλεσης του προγράµµατος.
6. Οι δυναµικές δοµές έχουν σταθερό µέγεθος

Λύση

1. Λ
2. Λ
3. Σ
4. Σ
5. Σ
6. Λ

Β. Ποιες είναι οι διαφορές µεταξύ µεταγλωττιστή (compiler) και διερµηνευτή (interpreter).
Μονάδες 10

Λύση

Σελίδα 137, παράγραφος 6.7

Γ. Η τιµή Α της βαθµολογίας σε ένα θέµα µπορεί να πάρει τις τιµές από 0 µέχρι και 20. (Το 0 και το 20 είναι επιτρεπτές τιµές). Ποια από τις παρακάτω λογικές εκφράσεις ελέγχει αυτή τη συνθήκη;
Μονάδες 5
i) Α >= 0 ή Α <= 20
ii) Α > 0 και Α <= 20
iii) Α >= 20 και Α <= 0
iv) Α >= 0 και Α <= 20

Λύση

Το σωστό είναι το iv

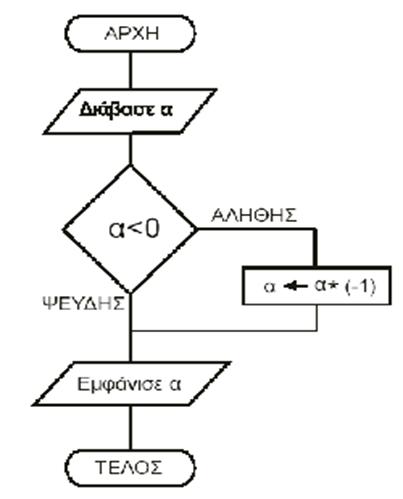
Δ. Ποιο είναι το αποτέλεσµα της εκτέλεσης του παρακάτω αλγορίθµου; Να αιτιολογήσετε την απάντησή σας.
Μονάδες 7

Λύση

Διαβάζει έναν αριθμό, υπολογίζει και εκτυπώνει την απόλυτη τιμή του

Ε. Να υπολογίσετε την τιµή της αριθµητικής έκφρασης Β * (Α DIV Β) + (Α MOD Β) για τις παρακάτω περιπτώσεις:
Μονάδες 6
i)   Α = 10 και Β = 5
ii)   Α = -5 και Β = 1
iii)  Α = 1 και Β = 5

Λύση

i) 5 * (10 DIV 5) + (10 MOD 5) = 5 * 2 + 0 = 10
ii) 1 * (-5 DIV 1) + (-5 MOD 1) = 1 * -5 + 0 = -5
iii) 5 * (1 DIV 5) + (1 MOD 5) = 5 * 0 + 1 = 1

ΘΕΜΑ 2ο
Δίνεται µονοδιάστατος πίνακας Α, 10 θέσεων, ο οποίος στις θέσεις 1 έως 10 περιέχει αντίστοιχα τους αριθµούς:   15, 3, 0, 5, 16, 2, 17, 8, 19, 1   και τµήµα αλγορίθµου:
Για i από 1 μέχρι 9 µε_βήµα 2
k ← ((i + 10) mod 10) + 1
Α[i] ← Α[k]
Εκτύπωσε i, k, A[i], A[k]
Τέλος_Επανάληψης
Ποιες τιµές τυπώνονται µε την εντολή     Εκτύπωσε i, k, A[i], A[k] καθώς εκτελείται το παραπάνω τµήµα αλγορίθµου;
Μονάδες 20

Λύση

i

k

  Πίνακας Α 

15

3

0

5

16

2

17

8

19

1

 1η επανάληψη

 1

2 

3

3

0

5

16

2

17

8

19

1

 2η επανάληψη

 3

 4

3

3

5

5

16

2

17

8

19

1

 3η επανάληψη

 5

 6

3

3

5

5

2

2

17

8

19

1

 4η επανάληψη

 7

 8

3

3

5

5

2

2

17

8

19

1

 5η επανάληψη

 9

 10

3

3

5

5

2

2

17

8

1

1

 11 

Θα εκτυπωθούν οι τιμές: 1 2 3 3,  3 4 5 5,  5 6 2 2,  7 8 8 8,  9 10 1 1

ΘΕΜΑ 3ο
Σε ένα κέντρο νεοσύλλεκτων υπάρχει η πρόθεση να δηµιουργηθούν δύο ειδικές διµοιρίες. Η διµοιρία Α θα αποτελείται από νεοσύλλεκτους πτυχιούχους τριτοβάθµιας εκπαίδευσης, ηλικίας από 24 έως και 28 χρόνων. Η διµοιρία Β θα αποτελείται από νεοσύλλεκτους απόφοιτους δευτεροβάθµιας εκπαίδευσης, ηλικίας από 18 έως και 24 χρόνων. Οι υπόλοιποι νεοσύλλεκτοι δεν κατατάσσονται σε καµία από αυτές τις διµοιρίες. Να αναπτύξετε αλγόριθµο ο οποίος:
α. διαβάζει το ονοµατεπώνυµο, την ηλικία και έναν αριθµό που καθορίζει το επίπεδο σπουδών του νεοσύλλεκτου και παίρνει τιµές από 1 έως 3 (1: τριτοβάθµια εκπαίδευση, 2: δευτεροβάθµια εκπαίδευση, 3: κάθε άλλη περίπτωση)
Μονάδες 5
β. εκτυπώνει:
i) το ονοµατεπώνυµο του νεοσύλλεκτου ii) το όνοµα της διµοιρίας (Α ή Β), εφόσον ο νεοσύλλεκτος κατατάσσεται σε µία από αυτές.
Μονάδες 15

Λύση

Αλγόριθμος Θέμα_3
 Διάβασε Ονοματεπώνυμο, ηλικία, επίπεδο_σπουδών ! ερώτημα α
 Εκτύπωσε Ονοματεπώνυμο
 Αν (ηλικία > 24) και (ηλικία <= 28) και (επίπεδο_σπουδών = 1) τότε ! ερώτημα β

   Εκτύπωσε "Διμοιρία Α"
 Αλλιώς_Αν (ηλικία > 18) και (ηλικία <= 24) και (επίπεδο_σπουδών = 2) τότε
 Εκτύπωσε "Διμοιρία Β"
 Τέλος_Αν
Τέλος Θέμα_3

ΘΕΜΑ 4ο
Μια αλυσίδα ξενοδοχείων έχει 5 ξενοδοχεία. Σε ένα µονοδιάστατο πίνακα ΞΕΝΟΔΟΧΕΙΑ[5] καταχωρούνται τα ονόµατα των ξενοδοχείων. Σε ένα άλλο δισδιάστατο πίνακα ΕΙΣΠΡΑΞΕΙΣ[5,12] καταχωρούνται οι εισπράξεις κάθε ξενοδοχείου για κάθε µήνα του έτους 2001, έτσι ώστε στην i γραµµή καταχωρούνται οι εισπράξεις του i ξενοδοχείου.
Να αναπτύξετε αλγόριθµο, ο οποίος:
α. διαβάζει τα στοιχεία των δύο πινάκων
Μονάδες 6
β. εκτυπώνει το όνοµα κάθε ξενοδοχείου και τις ετήσιες εισπράξεις του για το έτος 2001
Μονάδες 7
γ. εκτυπώνει το όνοµα του ξενοδοχείου µε τις µεγαλύτερες εισπράξεις για το έτος 2001.
Μονάδες 7

Λύση

Αλγόριθμος Θέμα_4
 Για i από 1 μέχρι 5 ! ερώτημα α
 Διάβασε ΞΕΝΟΔΟΧΕΙΑ[i]
 Τέλος_Επανάληψης
 Για i από 1 μέχρι 5
 Για j από 1 μέχρι 12
 Διάβασε ΕΙΣΡΑΞΕΙΣ[i, j]
 Τέλος_Επανάληψης
 Τέλος_Επανάληψης
 Για i από 1 μέχρι 5 ! ερώτημα β
 άθροισμα ← 0
 Για j από 1 μέχρι 6
 άθροισμα ← άθροισμα + ΕΙΣΡΑΞΕΙΣ[i, j]
 Τέλος_Επανάληψης
  ΕΤΗΣΙΕΣ_ΕΙΣΠΡΑΞΕΙΣ[i] ← άθροισμα
 Τέλος_Επανάληψης
 Για i από 1 μέχρι 5
 Εκτύπωσε ΞΕΝΟΔΟΧΕΙΑ[i], ΕΤΗΣΙΕΣ_ΕΙΣΠΡΑΞΕΙΣ[i]
 Τέλος_Επανάληψης
 μέγιστος ← ΕΤΗΣΙΕΣ_ΕΙΣΠΡΑΞΕΙΣ[1] ! ερώτημα γ
 θέση ← 1
 Για i από 2 μέχρι 5
 Αν ΕΤΗΣΙΕΣ_ΕΙΣΠΡΑΞΕΙΣ[i] > μέγιστος τότε
 μέγιστος ← ΕΤΗΣΙΕΣ_ΕΙΣΠΡΑΞΕΙΣ[i]
 θέση ← i
 Τέλος_Αν
 Τέλος_Επανάληψης
 Εκτύπωσε "Το ξενοδοχείο με τις περισσότερες εισπράξεις είναι ", ΞΕΝΟΔΟΧΕΙΑ[θέση]
Τέλος Θέμα_4