ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Δ΄ ΤΑΞΗΣ
ΕΣΠΕΡΙΝΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ
ΠΑΡΑΣΚΕΥΗ 6 ΙΟΥΝΙΟΥ 2003 - ΑΕΠΠ
ΘΕΜΑ 1ο
Α. Η «στοίβα» είναι
μια δομή δεδομένων.
1. Να περιγράψετε τη «στοίβα» με ένα παράδειγμα από την καθημερινή ζωή.
Μονάδες 6
2. Να περιγράψετε τις κύριες λειτουργίες της «στοίβας».
Μονάδες 4
|
Λύση |
|
1. Σελίδα 59,
παράγραφος 3.4 |
Β.
Οι εντολές που περιέχονται μέσα σε μια δομή επανάληψης της μορφής
ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ
Εντολή_1
Εντολή_2
...
Εντολή_ν
ΜΕΧΡΙΣ_ΟΤΟΥ <συνθήκη>
εκτελούνται τουλάχιστον μία φορά.
1. Είναι σωστή ή λανθασμένη η παραπάνω πρόταση;
Μονάδες 2
2. Να δικαιολογήσετε την απάντησή σας.
Μονάδες 3
|
Λύση |
|
1. Σωστή |
Γ.
Δίνεται ο αλγόριθμος:
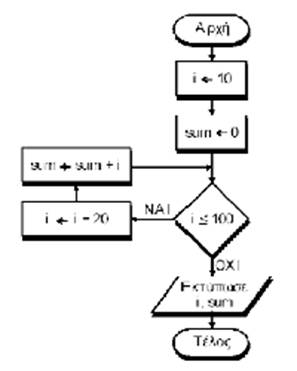
1.
Ποιον τύπο δεδομένων θα επιλέγατε για τη δήλωση κάθε μεταβλητής;
Μονάδες 2
2. Ποιες είναι οι διαδοχικές τιμές των i και sum;
Μονάδες 6
3. Ποιες τιμές θα εκτυπωθούν;
Μονάδες 3
4. Ποια αριθμητική παράσταση υπολογίζει ο αλγόριθμος;
Μονάδες 4
|
Λύση |
|||||||||||||||||||||||||||||||||||||||
|
1. Οι μεταβλητές i και sum είναι ακέραιες
Θα εκτυπωθούν οι τιμές i=110 και sum=350 Η παράσταση είναι 30 + 50 + 70 + 90 +
110 που ισούται με 350 |
Δ. Να μετατρέψετε το παρακάτω τμήμα αλγορίθμου σε ισοδύναμο με τη χρήση της
εντολής ΟΣΟ ... ΕΠΑΝΑΛΑΒΕ:
Μονάδες 10
Κ ← 0
ΓΙΑ Α ΑΠΟ 5 ΜΕΧΡΙ 100
ΜΕ_ΒΗΜΑ 10
Κ ← Κ + Α
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΓΡΑΨΕ Κ
|
Λύση |
K ← 0 A ← 5 ΟΣΟ (A <= 100) ΕΠΑΝΑΛΑΒΕ K ← K + A A ← A + 10 ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ ΓΡΑΨΕ K |
ΘΕΜΑ 2ο
Δίνεται ο πίνακας Α
(σχήμα 1) και το παρακάτω τμήμα προγράμματος:
sum ← 0
ΓΙΑ i ΑΠΟ 1 ΜΕΧΡΙ
5
ΓΙΑ j ΑΠΟ
1 ΜΕΧΡΙ 5
ΑΝ i = j TOTE
sum ← sum + A[i,j]
AΛΛΙΩΣ
A[i,j] ← 0
ΤΕΛΟΣ_ΑΝ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΓΡΑΨΕ sum
Αυτό το τμήμα προγράμματος χρησιμοποιεί τον πίνακα Α, με τις τιμές των
στοιχείων του, όπως αυτές φαίνονται στο σχήμα 1.
|
1 |
-1 |
7 |
1 |
1 |
|
6 |
2 |
0 |
8 |
-2 |
|
4 |
9 |
3 |
3 |
0 |
|
3 |
5 |
-4 |
2 |
1 |
|
0 |
1 |
2 |
0 |
1 |
Σχήμα 1: Πίνακας Α
1.
Να σχεδιάσετε στο τετράδιό σας τον πίνακα Α με τις τιμές που θα έχουν τα
στοιχεία του, μετά την εκτέλεση του τμήματος προγράμματος.
Μονάδες 15
2. Ποια είναι η τιμή της μεταβλητής sum που θα
εμφανιστεί;
Μονάδες 5
|
Λύση |
|||||||||||||||||||||||||
Όλα τα στοιχεία εκτός κυρίας διαγωνίου
θα μηδενιστούν Το άθροισμα των στοιχείων της κυρίας
διαγωνίου, η τιμή 9 |
ΘΕΜΑ 3ο
Για κάθε υπάλληλο
δίνονται: ο μηνιαίος βασικός μισθός και ο αριθμός των παιδιών του. Δεχόμαστε
ότι ο υπάλληλος μπορεί να έχει μέχρι και 20 παιδιά και ότι ο μηνιαίος βασικός
μισθός του κυμαίνεται από 500 μέχρι και 1000 ευρώ.
Οι συνολικές αποδοχές του υπολογίζονται ως το άθροισμα του μηνιαίου
βασικού μισθού και του οικογενειακού επιδόματός του. Το οικογενειακό
επίδομα υπολογίζεται ως εξής:
30 ευρώ για κάθε παιδί μέχρι και τρία παιδιά, και 40 ευρώ για κάθε παιδί πέραν των τριών (4ο, 5ο, 6ο κ.τ.λ.).
α. Να προσδιορίσετε τις μεταβλητές που θα χρησιμοποιήσετε και να δηλώσετε τον
τύπο των δεδομένων που αντιστοιχούν σ' αυτές.
Μονάδες 4
β. Να γράψετε αλγόριθμο, ο οποίος:
1. εισάγει τα κατάλληλα δεδομένα και ελέγχει την ορθή καταχώρισή τους,
Μονάδες 7
2. υπολογίζει και εμφανίζει το οικογενειακό επίδομα και
Μονάδες 7
3. υπολογίζει και εμφανίζει τις συνολικές αποδοχές του υπαλλήλου.
Μονάδες 2
|
Λύση |
|
Ακέραιες μεταβλητές: αριθμός_παιδιών Αλγόριθμος Θέμα_3 Αρχή_Επανάληψης Διάβασε βασικός_μισθός ! ερώτημα β1 Μέχρις_Ότου (βασικός_μισθός >= 500) και (βασικός_μισθός <= 1000) Αρχή_Επανάληψης Διάβασε αριθμός_παιδιών Μέχρις_Ότου (αριθμός_παιδιών >= 0) και (αριθμός_παιδιών <= 20) Αν αριθμός_παιδιών <= 3 τότε ! ερώτημα β2 οικογενειακό_επίδομα ← αριθμός_παιδιών * 30 Αλλιώς οικογενειακό_επίδομα ← 3 * 30 + (αριθμός_παιδιών - 3) * 40 Τέλος_Αν Εμφανισε "Το οικογενειακό επίδομα είναι ", οικογενειακό_επίδομα μισθός ← βασικός_μισθός + οικογενειακό_επίδομα ! ερώτημα β3 Εμφανισε "ο τελικός μισθός είναι ", μισθός Τέλος Θέμα_3 |
ΘΕΜΑ 4ο
Για κάθε μαθητή
δίνονται τα στοιχεία: ονοματεπώνυμο, προφορικός και γραπτός βαθμός ενός
μαθήματος. Να γραφεί αλγόριθμος, ο οποίος εκτελεί τις ακόλουθες λειτουργίες:
α. Διαβάζει τα στοιχεία πολλών μαθητών και σταματά όταν δοθεί ως ονοματεπώνυμο
το κενό.
Μονάδες 5
β. Ελέγχει αν ο προφορικός και ο γραπτός βαθμός είναι από 0 μέχρι και 20.
Μονάδες 5
γ. Υπολογίζει τον τελικό βαθμό του μαθήματος, ο οποίος είναι το άθροισμα του
30% του προφορικού βαθμού και του 70% του γραπτού βαθμού. Επίσης, τυπώνει το
ονοματεπώνυμο του μαθητή και τον τελικό βαθμό του μαθήματος.
Μονάδες 5
δ. Υπολογίζει και τυπώνει το ποσοστό των μαθητών που έχουν βαθμό μεγαλύτερο του
18.
Μονάδες 5
|
Λύση |
Αλγόριθμος Θέμα_4 πλήθος ← 0 μεγ_18 ← 0 Διάβασε όνομα Όσο (όνομα <> "") επανάλαβε ! ερώτημα α Αρχή_Επανάληψης ! ερώτημα β Διάβασε προφορικός_βαθμός Μέχρις_Ότου (προφορικός_βαθμός >= 0) και (προφορικός_βαθμός <= 20) Αρχή_Επανάληψης Διάβασε γραπτός_βαθμός Μέχρις_Ότου (γραπτός_βαθμός >= 0) και (γραπτός_βαθμός <= 20) τελικός_βαθμός ← 0.3 * προφορικός_βαθμός + 0.7 * γραπτός_βαθμός ! ερώτημα γ Εκτύπωσε "Ο τελικός βαθμός του μαθητή ", όνομα, "είναι: ", τελικός_βαθμός Αν τελικός_βαθμός > 18 τότε μεγ_18 ← μεγ_18 + 1 Τέλος_Αν πλήθος ← πλήθος + 1 Διάβασε όνομα Τέλος_Επανάληψης Αν πλήθος = 0 τότε ! ερώτημα δ Εκτύπωσε "Δεν δόθηκε κανένα όνομα" Αλλιώς ποσοστό ← 100 * (μεγ_18 / Πλήθος) Εκτύπωσε "Το ποσοστό των μαθητών με βαθμό μεγαλύτερο του 18 είναι: ", ποσοστό Τέλος_Αν Τέλος Θέμα_4 |