ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Δ΄ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ
ΔΕΥΤΕΡΑ 7 ΙΟΥΝΙΟΥ 2004 - ΑΕΠΠ

ΘΕΜΑ 1ο
Α. Στον προγρα΅΅ατισ΅ό χρησι΅οποιούνται δο΅ές δεδο΅ένων.
1. Τι είναι δυνα΅ική δο΅ή δεδο΅ένων;
Μονάδες 3
2. Τι είναι στατική δο΅ή δεδο΅ένων;
Μονάδες 3
3. Να αναφερθούν οι βασικές λειτουργίες (πράξεις) επί των δο΅ών δεδο΅ένων.
Μονάδες 8

Λύση

Α. Σελίδα 56, παράγραφος 3.2

Β. Η ουρά είναι ΅ία δο΅ή δεδο΅ένων.
1. Να δώσετε ένα παράδειγ΅α ουράς από την καθη΅ερινή ζωή.
Μονάδες 3
2. Να αναφέρετε τις λειτουργίες της ουράς και τους δείκτες που απαιτούνται.
Μονάδες 3
3. Σε ΅ία ουρά 10 θέσεων έχουν τοποθετηθεί διαδοχικά τα στοιχεία: Μ, Κ, ∆, Α, Σ στην πρώτη, δεύτερη, τρίτη, τέταρτη και πέ΅πτη θέση αντίστοιχα.
α. Να προσδιορίσετε τις τι΅ές των δεικτών της παραπάνω ουράς.
Μονάδες 3
β. Στη συνέχεια να αφαιρέσετε ένα στοιχείο από την ουρά. Ποιος δείκτης ΅εταβάλλεται και ποια η νέα του τι΅ή;
Μονάδες 3
γ. Τέλος να τοποθετήσετε το στοιχείο Λ στην ουρά. Ποιος δείκτης ΅εταβάλλεται και ποια η νέα του τι΅ή;
Μονάδες 3

Λύση

1-2. Σελίδα 60, παράγραφος 3.5
3. α. εμπρός = 1, πίσω = 5
      β. εμπρός = 2
      γ. πίσω = 6

Γ. Οι εντολές που περιέχονται μέσα σε μια δομή επανάληψης της μορφής
        Χ ← 50
        ΟΣΟ Χ > 0 ΕΠΑΝΑΛΑΒΕ
            ΓΙΑ Υ ΑΠΟ 2 ΜΕΧΡΙ 6 ΜΕ_ΒΗΜΑ 2
                  Χ ← Χ - 10
            ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
            ΓΡΑΨΕ Χ
        ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
1. Πόσες φορές θα εκτελεστεί η εντολή ΓΡΑΨΕ Χ;
Μονάδες 3
2. Πόσες φορές θα εκτελεστεί η εντολή εκχώρησης Χ ← Χ - 10;
Μονάδες 3
3. Ποιες είναι οι διαδοχικές τι΅ές των ΅εταβλητών Χ και Υ σε όλες τις επαναλήψεις;
Μονάδες 5

Λύση

1. 2 φορές
2. 6 φορές

 

 Χ 

 Υ 

 Αρχικοποίηση

 50 

 

 50 > 0 1η επανάληψη  

 

 

  1η επανάληψη Για   

40

2

  2η επανάληψη Για   

30

4

  3η επανάληψη Για   

20

6

  τερματισμός επανάληψης Για   

 

8

 20 > 0 2η επανάληψη  

 

 

  1η επανάληψη Για   

10

2

  2η επανάληψη Για   

0

4

  3η επανάληψη Για   

-10

6

  τερματισμός επανάληψης Για   

 

8

 -10> 0 Ψευδής - τερματισμός επανάληψης  

 

 

Θα εκτυπωθούν οι τιμές  20, -10

ΘΕΜΑ 2ο
Δίνεται το διάγραμμα ροής:

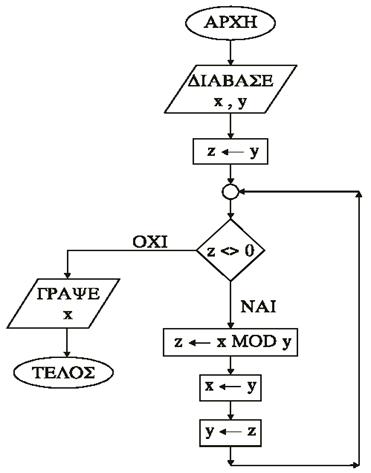
1. Να γράψετε τον πίνακα τι΅ών των ΅εταβλητών x, y, z αν ως αρχικές τι΅ές δοθούν x = 12 και y = 18.
Μονάδες 10
2. Να ΅ετατρέψετε το παραπάνω διάγρα΅΅α ροής σε πρόγρα΅΅α.
Τ΅ή΅α δηλώσεων
Μονάδες 2
Κύριο μέρος.
Μονάδες 8

Λύση

 

 Χ 

 Υ 

 Ζ 

 Αρχικοποίηση

 12 

18

18

 18 <> 0 1η επανάληψη

18

12

12

 12 <> 0 2η επανάληψη

12

6

6

 6 <> 0 3η επανάληψη

6

0

0

 0 <> 0 τερματισμός επανάληψης

 

 

 

Θα εκτυπωθεί η τιμή 6

 
ΠΡΟΓΡΑΜΜΑ Θέμα_2
ΜΕΤΑΒΛΗΤΕΣ
  ΑΚΕΡΑΙΕΣ: x, y, z
ΑΡΧΗ
  ΔΙΑΒΑΣΕ x, y
  z <– y
  ΟΣΟ (z <> y) ΕΠΑΝΑΛΑΒΕ
    z <– x MOD y
    x <– y
    y <– z
  ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
  ΓΡΑΨΕ x
ΤΕΛΟΣ_ΠΡΟΓΡΑΜΜΑΤΟΣ

ΘΕΜΑ 3ο
Σε έναν αγώνα δισκοβολίας συ΅΅ετέχουν 20 αθλητές. Κάθε αθλητής έκανε ΅όνο ΅ία έγκυρη ρίψη που καταχωρείται ως επίδοση του αθλητή και εκφράζεται σε ΅έτρα. Να αναπτύξετε αλγόριθ΅ο που:
α. να διαβάζει για κάθε αθλητή το όνο΅α και την επίδοσή του,
Μονάδες 5
β. να ταξινο΅εί τους αθλητές ως προς την επίδοσή τους,
Μονάδες 5
γ. να ε΅φανίζει τα ονό΅ατα και τις επιδόσεις των τριών πρώτων αθλητών, αρχίζοντας από εκείνον ΅ε την καλύτερη επίδοση,
Μονάδες 5
δ. να ε΅φανίζει τα ονό΅ατα και τις επιδόσεις των πέντε τελευταίων αθλητών, αρχίζοντας από εκείνον ΅ε την καλύτερη επίδοση.
Μονάδες 5
Ση΅είωση: Να θεωρήσετε ότι δεν υπάρχουν αθλητές ΅ε την ίδια ακριβώς επίδοση

Λύση

 
Αλγόριθμος Θέμα_3
  Για i από 1 μέχρι 20 ! ερώτημα α
    Διάβασε ΟΝΟΜΑ[i]
    Αρχή_Επανάληψης
      Διάβασε ΕΠΙΔΟΣΗ[i]
    Μέχρις_Ότου (ΕΠΙΔΟΣΗ[i] >= 0)
  Τέλος_Επανάληψης
  Για i από 2 μέχρι 20 ! ερώτημα β
    Για j από 20 μέχρι i με_βήμα -1 ! φθίνουσα ταξινόμηση
      Αν ΕΠΙΔΟΣΗ[j-1] < ΕΠΙΔΟΣΗ[j] τότε
        βοηθητική ← ΕΠΙΔΟΣΗ[j-1]
        ΕΠΙΔΟΣΗ[j-1] ← ΕΠΙΔΟΣΗ[j]
        ΕΠΙΔΟΣΗ[j] ← βοηθητική
        βοηθητική1 ← ΟΝΟΜΑ[j-1]
        ΟΝΟΜΑ[j-1] ← ΟΝΟΜΑ[j]
        ΟΝΟΜΑ[j] ← βοηθητική1
      Τέλος_Αν
    Τέλος_Επανάληψης
  Τέλος_Επανάληψης
  ! ερώτημα γ
  Για i από 1 μέχρι 3   ! 3 πρώτοι
    Εκτύπωσε ΟΝΟΜΑ[i], ΕΠΙΔΟΣΗ[i]
  Τέλος_Επανάληψης
  ! ερώτημα δ
  Για i από 20 μέχρι 16  ! 5 τελευταίοι
    Εκτύπωσε ΟΝΟΜΑ[i], ΕΠΙΔΟΣΗ[i]
  Τέλος_Επανάληψης
 Τέλος Θέμα_3

ΘΕΜΑ 4ο
Μία εταιρεία απασχολεί 30 υπαλλήλους. Οι ΅ηνιαίες αποδοχές κάθε υπαλλήλου κυ΅αίνονται από 0 € έως και 3.000 €.
Α. Να γράψετε αλγόριθ΅ο που για κάθε υπάλληλο:
1. να διαβάζει το ονο΅ατεπώνυ΅ο και τις ΅ηνιαίες αποδοχές και να ελέγχει την ορθότητα καταχώρησης των ΅ηνιαίων αποδοχών του,
Μονάδες 4
2. να υπολογίζει το ποσό του φόρου κλι΅ακωτά, σύ΅φωνα ΅ε τον παρακάτω πίνακα:
Μονάδες 8

  Μηνιαίες Αποδοχές   

   Ποσοστό κράτησης φόρου 

Έως και 700 €

0 %

  ’νω των 700 € έως και 1.000 €   

15 %

  ’νω των 1.000 € έως και 1.700 €   

30 %

’νω των 1.700 €

40 %

3. να ε΅φανίζει το ονο΅ατεπώνυ΅ο, τις ΅ηνιαίες αποδοχές, το φόρο και τις καθαρές ΅ηνιαίες αποδοχές, που προκύπτουν ΅ετά την αφαίρεση του φόρου.
Μονάδες 4
Β. Τέλος, ο παραπάνω αλγόριθ΅ος να υπολογίζει και να ε΅φανίζει
1. το συνολικό ποσό που αντιστοιχεί στο φόρο όλων των υπαλλήλων,
Μονάδες 2
2. το συνολικό ποσό που αντιστοιχεί στις καθαρές ΅ηνιαίες αποδοχές όλων των υπαλλήλων.
Μονάδες 2

Λύση

 
Αλγόριθμος Θέμα_4
  Συνολικός_φόρος ← 0
  Σύνολικές_καθαρές_αποδοχές ← 0
  Για i από 1 μέχρι 30
    Διάβασε όνομα ! ερώτημα Α1
    Αρχή_Επανάληψης
      Διάβασε μηνιαίες_αποδοχές
    Μέχρις_Ότου (μηνιαίες_αποδοχές >= 0) και (μηνιαίες_αποδοχές <= 3000)
    Αν (μηνιαίες_αποδοχές <= 700) τότε ! ερώτημα Α2

      φόρος ← 0
    Αλλιώς_Αν (μηνιαίες_αποδοχές <= 1000) τότε

      φόρος ← 0 + (μηνιαίες_αποδοχές - 700) * 0.15
    Αλλιώς_Αν (μηνιαίες_αποδοχές <= 1700) τότε

      φόρος ← 0 + 0.15 * 300 + (μηνιαίες_αποδοχές - 1000) * 0.30
    Αλλιώς
      φόρος ← 0 + 0.15 * 300 + 0.30 * 700 + (μηνιαίες_αποδοχές - 1700) * 0.40
    Τέλος_Αν
    καθαρές_αποδοχές ← μηνιαίες_αποδοχές - φόρος
    Εμφάνισε όνομα, μηνιαίες_αποδοχές, φόρος, καθαρές_αποδοχές ! ερώτημα Α3
    Συνολικός_φόρος ← Συνολικός_φόρος + φόρος ! ερώτημα Β1
    Σύνολικές_καθαρές_αποδοχές ← Σύνολικές_καθαρές_αποδοχές + καθαρές_αποδοχές ! ερώτημα Β2
  Τέλος_Επανάληψης
  Εμφάνισε Συνολικός_φόρος, Σύνολικές_καθαρές_αποδοχές
Τέλος Θέμα_4